Capítulo 7 Árboles binarios de búsqueda (ABB):

7.1 Definición

Se trata de árboles de orden 2 en los que se cumple que para cada nodo, el valor de la clave de la raíz del subárbol izquierdo es menor que el valor de la clave del nodo y que el valor de la clave raíz del subárbol derecho es mayor que el valor de la clave del nodo.

7.2 Operaciones en ABB

El repertorio de operaciones que se pueden realizar sobre un ABB es parecido al que realizábamos sobre otras estructuras de datos, más alguna otra propia de árboles:

Buscar un elemento.
Insertar un elemento.
Borrar un elemento.
Movimientos a través del árbol:
- Izquierda.
- Derecha.
- Raiz.
Información:
- Comprobar si un árbol está vacío.
- Calcular el número de nodos.
- Comprobar si el nodo es hoja.
- Calcular la altura de un nodo.
- Calcular la altura de un árbol.

7.3 Buscar un elemento

Partiendo siempre del nodo raíz, el modo de buscar un elemento se define de forma recursiva.

Si el árbol está vacío, terminamos la búsqueda: el elemento no está en el árbol.
Si el valor del nodo raíz es igual que el del elemento que buscamos, terminamos la búsqueda con éxito.
Si el valor del nodo raíz es mayor que el elemento que buscamos, continuaremos la búsqueda en el árbol izquierdo.
Si el valor del nodo raíz es menor que el elemento que buscamos, continuaremos la búsqueda en el árbol derecho.

El valor de retorno de una función de búsqueda en un ABB puede ser un puntero al nodo encontrado, o NULL, si no se ha encontrado.

7.4 Insertar un elemento

Para insertar un elemento nos basamos en el algoritmo de búsqueda. Si el elemento está en el árbol no lo insertaremos. Si no lo está, lo insertaremos a continuación del último nodo visitado.

Necesitamos un puntero auxiliar para conservar una referencia al padre del nodo raíz actual. El valor inicial para ese puntero es NULL.

Padre = NULL
nodo = Raiz
Bucle: mientras actual no sea un árbol vacío o hasta que se encuentre el elemento.
- Si el valor del nodo raíz es mayor que el elemento que buscamos, continuaremos la búsqueda en el árbol izquierdo: Padre=nodo, nodo=nodo->izquierdo.
- Si el valor del nodo raíz es menor que el elemento que buscamos, continuaremos la búsqueda en el árbol derecho: Padre=nodo, nodo=nodo->derecho.
Si nodo no es NULL, el elemento está en el árbol, por lo tanto salimos.
Si Padre es NULL, el árbol estaba vacío, por lo tanto, el nuevo árbol sólo contendrá el nuevo elemento, que será la raíz del árbol.
Si el elemento es menor que el Padre, entonces insertamos el nuevo elemento como un nuevo árbol izquierdo de Padre.
Si el elemento es mayor que el Padre, entonces insertamos el nuevo elemento como un nuevo árbol derecho de Padre.

Este modo de actuar asegura que el árbol sigue siendo ABB.

7.5 Borrar un elemento

Para borrar un elemento también nos basamos en el algoritmo de búsqueda. Si el elemento no está en el árbol no lo podremos borrar. Si está, hay dos casos posibles:

Se trata de un nodo hoja: en ese caso lo borraremos directamente.
Se trata de un nodo rama: en ese caso no podemos eliminarlo, puesto que perderíamos todos los elementos del árbol de que el nodo actual es padre. En su lugar buscamos el nodo más a la izquierda del subárbol derecho, o el más a la derecha del subárbol izquierdo e intercambiamos sus valores. A continuación eliminamos el nodo hoja.

Necesitamos un puntero auxiliar para conservar una referencia al padre del nodo raíz actual. El valor inicial para ese puntero es NULL.

Padre = NULL
Si el árbol está vacío: el elemento no está en el árbol, por lo tanto salimos sin eliminar ningún elemento.
(1) Si el valor del nodo raíz es igual que el del elemento que buscamos, estamos ante uno de los siguientes casos:
- El nodo raíz es un nodo hoja:
  - Si 'Padre' es NULL, el nodo raíz es el único del árbol, por lo tanto el puntero al árbol debe ser NULL.
  - Si raíz es la rama derecha de 'Padre', hacemos que esa rama apunte a NULL.
  - Si raíz es la rama izquierda de 'Padre', hacemos que esa rama apunte a NULL.
  - Eliminamos el nodo, y salimos.
- El nodo no es un nodo hoja:
  - Buscamos el 'nodo' más a la izquierda del árbol derecho de raíz o el más a la derecha del árbol izquierdo. Hay que tener en cuenta que puede que sólo exista uno de esos árboles. Al mismo tiempo, actualizamos 'Padre' para que apunte al padre de 'nodo'.
  - Intercambiamos los elementos de los nodos raíz y 'nodo'.
  - Borramos el nodo 'nodo'. Esto significa volver a (1), ya que puede suceder que 'nodo' no sea un nodo hoja. (Ver ejemplo 3)
Si el valor del nodo raíz es mayor que el elemento que buscamos, continuaremos la búsqueda en el árbol izquierdo.
Si el valor del nodo raíz es menor que el elemento que buscamos, continuaremos la búsqueda en el árbol derecho.

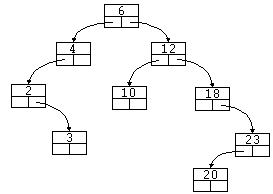
Ejemplo 1: Borrar un nodo hoja

En el árbol de ejemplo, borrar el nodo 3.

Localizamos el nodo a borrar, al tiempo que mantenemos un puntero a 'Padre'.
Hacemos que el puntero de 'Padre' que apuntaba a 'nodo', ahora apunte a NULL.
Borramos el 'nodo'.

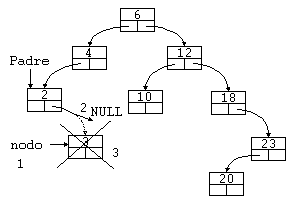
Ejemplo 2: Borrar un nodo rama con intercambio de un nodo hoja.

En el árbol de ejemplo, borrar el nodo 4.

Localizamos el nodo a borrar ('raíz').
Buscamos el nodo más a la derecha del árbol izquierdo de 'raíz', en este caso el 3, al tiempo que mantenemos un puntero a 'Padre' a 'nodo'.
Intercambiamos los elementos 3 y 4.
Hacemos que el puntero de 'Padre' que apuntaba a 'nodo', ahora apunte a NULL.
Borramos el 'nodo'.

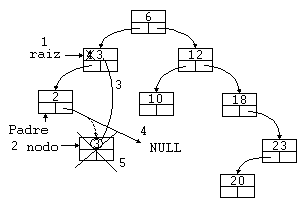
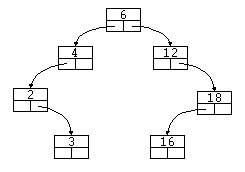
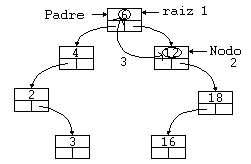
Ejemplo 3: Borrar un nodo rama con intercambio de un nodo rama.

Para este ejemplo usaremos otro árbol. En éste borraremos el elemento 6.

Localizamos el nodo a borrar ('raíz').
Buscamos el nodo más a la izquierda del árbol derecho de 'raíz', en este caso el 12, ya que el árbol derecho no tiene nodos a su izquierda, si optamos por la rama izquierda, estaremos en un caso análogo. Al mismo tiempo que mantenemos un puntero a 'Padre' a 'nodo'.
Intercambiamos los elementos 6 y 12.
Ahora tenemos que repetir el bucle para el nodo 6 de nuevo, ya que no podemos eliminarlo.
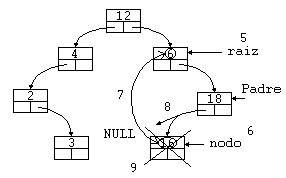
Localizamos de nuevo el nodo a borrar ('raíz').
Buscamos el nodo más a la izquierda del árbol derecho de 'raíz', en este caso el 16, al mismo tiempo que mantenemos un puntero a 'Padre' a 'nodo'.
Intercambiamos los elementos 6 y 16.
Hacemos que el puntero de 'Padre' que apuntaba a 'nodo', ahora apunte a NULL.
Borramos el 'nodo'.

Este modo de actuar asegura que el árbol sigue siendo ABB.